ПСКОВСКИЙ
ВОЛЬНЫЙ ИНСТИТУТ
РЕКОМЕНДАЦИИ ПО МАТЕМАТИКЕ
для
студентов заочного отделения
1
курса
специальности
«Финансы и кредит», «Психология»
Составила к.ф.-м.н. В.А.Фахретдинова
ПСКОВ 2004
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Главная цель курса
«Математика» создать фундамент математического и естественно-научного
образования студента. Курс
предоставляет студентам необходимые знания и достаточную практическую
подготовку для последующего использования математических методов. Цель изучения дисциплины «Математика» состоит в том, чтобы вооружить
будущего специалиста мощным инструментом, который он может использовать при
решении фундаментальных научных и прикладных задач, учитывать
математические методы в своей повседневной деятельности и руководствоваться ими
при принятии управленческих решений.
Курс математики на 1 курсе включает 3 раздела: «Элементы линейной
алгебры», «Элементы аналитической геометрии», «Основы математического анализа».
В данной части курса обобщается основное содержание школьных курсов
элементарной алгебры, геометрии и математического анализа.
Основные умения и навыки,
которыми должны овладеть студенты:
Тема 1 «Элементы линейной алгебры».
Необходимо освоить понятия
матрицы, определителя квадратной матрицы, системы линейных уравнений. Знать
условия совместности и несовместности системы линейных уравнений.
Освоить операции над
матрицами (сложение, вычитание, умножение на число, умножение матриц),
вычисление определителей 2-го и 3-го порядков. Уметь решать системы линейных
уравнений методом Гаусса и методом Крамера.
Тема 2 «Элементы аналитической геометрии».
Необходимо знать понятие
вектора и определение скалярного произведения векторов, геометрический смысл
векторного и смешанного произведения векторов. Знать уравнения прямых и
плоскостей в пространстве. Условия перпендикулярности и параллельности.
Уметь вычислять скалярное,
векторное, смешанное произведение векторов в координатах. Уметь находить
уравнение прямой или плоскости по заданным условиям. Уметь определять угол
между прямыми и плоскостями, вычислять площадь грани и объем треугольной
пирамиды (параллелепипеда).
Тема 3 «Основы математического анализа».
Необходимо иметь
представление о множествах и операциях над ними. Знать числовые множества.
Знать элементарные функции, их свойства и графики. Знать определение
производной и ее геометрический смысл, основные теоремы дифференцирования.
Знать определение первообразной и неопределенного интеграла. Знать определенный
интеграл и его геометрический смысл.
Уметь строить графики функций, выполнять преобразования графиков. Уметь вычислять производные. Уметь вычислять некоторые типы неопределенных интегралов. Уметь применять формулу Ньютона-Лейбница для вычисления определенного интеграла.
По курсу предлагается 4
контрольные работы. Первая по линейной алгебре, вторая по геометрии, третья по
дифференциальному исчислению и четвертая по интегральному исчислению.
Контрольные работы №1, №2
сдаются в первом семестре за 2 недели до зачета. На зачете студент должен
продемонстрировать знание основных понятий и умение решать задачи по первым
двум темам.
Контрольные работы №3, №4
сдаются во втором семестре за 2 недели до экзамена. На экзамене студент должен
осветить один из вопросов (список прилагается), а также продемонстрировать
умение решать задачи по третьей теме.
Замечание.
Условия
заданий контрольных работ содержат буквы m и n. Вместо них необходимо подставить конкретные числа.
Число m определяется следующим образом: определить номер
буквы в алфавите, с которой начинается Ваша фамилия. Аналогично определяется n, но берется номер
буквы, с которой начинается имя. Например: Васильева Ирина – m =
3, n = 10.
Контрольная работа №1
1.
Даны
матрицы А =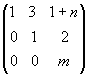 , В =
, В = 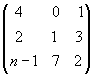 .
.
Выполнить операции над матрицами
а) (2+n)А – mВ; б) Вычислить АВ и BA.
Убедиться, что АВ ¹ BA.
2.
Вычислить
определитель матрицы В по правилу «треугольника» и по теореме Лапласа.
3.
Решить
систему уравнений а) методом Гаусса, б)
методом Крамера
mx + 3y – z = m - 1
x – ny + z = 2
3x + y – nz
= 3 – n
Контрольная работа №2
Даны вершины треугольной пирамиды
А (m, n+1, 0), B (-n, 1, 2-m), C (-2, 0, n-m), D (0, -m, n+2).
Найти:
а) уравнения плоскостей всех граней пирамиды;
б) уравнения всех прямых, содержащих ребра;
в) уравнение высоты DH на плоскость основания АВС;
г) уравнение медианы АК грани АВС;
д) уравнение
плоскости, проходящей через точку В, параллельно грани АСD;
е) площадь основания АВС;
ж) объем пирамиды ABCD;
з) длину высоты DH;
и) косинус
угла между прямыми АВ и CD.
Контрольная работа № 3
1.
Используя
преобразования графиков элементарных функций
![]() построить графики функций
построить графики функций
![]()
2.
Найти производные ![]() функций
функций
1) 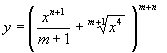 ; 2)
; 2) 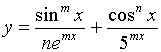 ;
;
3) ![]() ; 4)
; 4)
![]()
2.
Найти
наибольшее и наименьшее значение функции
![]() на отрезке
на отрезке ![]() .
.
Контрольная работа по математике № 4
1. Вычислить интегралы
a)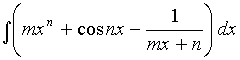 d)
d) 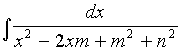
b) 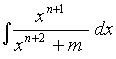 e)
e) 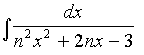
c) ![]() f)
f) ![]()
3.
Построить чертеж и найти площадь
криволинейной трапеции, ограниченной
линиями 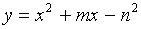 и
и 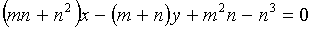 .
.
Вопросы к экзамену
1.
Определение
матрицы. Виды матриц. Операции над матрицами.
2.
Определители
второго и третьего порядка.
3.
Системы
линейных уравнений. Основные понятия,
4.
Решение
систем линейных уравнений методом Гаусса.
5.
Решение
систем линейных уравнений методом Крамера.
6.
Векторы.
Операции над векторами. Коллинеарные и компланарные векторы.
7.
Координаты
вектора. Скалярное произведение. Длина вектора.
8.
Координаты
точки. Системы координат. Расстояние между точками.
9.
Уравнение
плоскости в пространстве.
10.
Уравнение
прямой в пространстве.
11.
Векторное
произведение векторов. Свойства векторного произведения.
12.
Выражение
векторного произведения в координатах. Задача о вычисление площади
параллелограмма.
13.
Смешанное
произведение векторов. Геометрический смысл смешанного произведения. Задача о
вычислении объема параллелепипеда.
14.
Множества.
Операции над множествами. Числовые множества.
15.
Элементарные
функции и их графики.
16.
Производная:
определение, геометрический смысл.
17.
Правила дифференцирования. Таблица
производных.
18.
Дифференцирование сложной функции. Основные
теоремы дифференцирования.
19.
Исследование
функций и построение графиков.
20.
Первообразная
и неопределенный интеграл.
21.
Методы
интегрирования.
22.
Определенный
интеграл. Формула Ньютона-Лейбница.
23.
Вычисление
площади криволинейной трапеции с помощью определенного интеграла.
литература.
1.
Гусак
А.А. Высшая математика. Т.1: Учебн.пособие для студентов вузов. – Минск.: Тетра
Системс. 1998. –544с.
2.
Гусак
А.А. Высшая математика. Т.2: Учебн.пособие для студентов вузов. – Минск.: Тетра
Системс. 1998. –448с.
3.
Данко
П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах,
чч. 1,2, Высшая школа. - М: 1980.
4.
Кремер
Н.Ш. Высшая математика для экономистов: Учебник для вузов. – М.: Банки и биржи,
ЮНИТИ, 1998. – 471с.
5.
Сборник
задач по высшей математике для экономистов: Уч.пособие / под ред.В.И.Ермакова.
– М.: ИНФРА- М, 2002. – 575с.
6.
Щипачев
В.С. Высшая математика. Учебник для вузов. – М: Высшая школа, 2001. – 479с.
7.
Щипачев
В.С. Задачник по высшей математике: Учеб.пособие для вузов. – М. Высшая школа,
2001. – 304с.